
2017年成人高等学校高起点招生全国统一考试
数 学
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间150分钟。
第I卷(选择题,共85分)
一、选择题(本大题共17小题,每小题5分,共85分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合M={1,2,3,4,5),N={2,4,6),则M∩N=( )
A.{2,4) B.(2,4,6) C.(1,3,5) D.{1,2,3,4.5,6)
2.函数y=3sin 的最小正周期是( )
的最小正周期是( )
A.8π B.4π C.2π D.2π
3.函数y=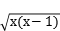 的定义城为( )
的定义城为( )
A.{x|x 0} B.{x|x
0} B.{x|x 1} C.{x|
1} C.{x| x
x 1} D.{x|
1} D.{x|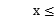 0
0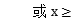 1}
1}
4.设a,b,c为实数,且a>b,则( )
A.a-c>b-c B.|a|>|b| C. >
> D.ac>bc
D.ac>bc
5.若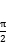 <
< <
< ,且sin
,且sin =
= ,则
,则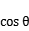 =( )
=( )
A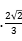 B.
B.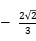 C.
C.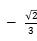 D.
D.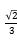
 6.函数y=6sinxcosc的最大值为( )
6.函数y=6sinxcosc的最大值为( )
A.1 B.2 C.6 D.3
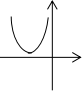
7.右图是二次函数y=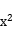 +bx+c的部分图像,则( )
+bx+c的部分图像,则( )
A.b>0,c>0 B.b>0,c<0 C.b<0,c>0 D.b<0,c<0 0
8.已知点A(4,1),B(2,3),则线段AB的垂直平分线方程为( )
A.x-y+1=0 B.x+y-5=0 C.x-y-1=0 D.x-2y+1=0
9.函数y= 是( )
是( )
A.奇函数,且在(0,+ )单调递增 B.偶函数,且在(0,+
)单调递增 B.偶函数,且在(0,+ )单调递减
)单调递减
C.奇函数,且在(- ,0)单调递减 D.偶函数,且在(-
,0)单调递减 D.偶函数,且在(- ,0)单调递增
,0)单调递增
10.一个圆上有5个不同的点,以这5个点中任意3个为顶点的三角形共有( )
A.60个 B.15个 C.5个 D.10个
11.若lg5=m,则lg2=( )
A.5m B.1-m C.2m D.m+1
12.设f(x+1)=x(x+1),则f(2)= ( )
A.1 B.3 C.2 D.6
13.函数y=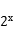 的图像与直线x+3=0的交点坐标为( )
的图像与直线x+3=0的交点坐标为( )
A.(-3,-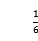 ) B.(-3,
) B.(-3,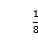 ) C.(-3,
) C.(-3,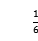 ) D.(-3,-
) D.(-3,-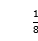 )
)
14.双曲线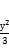 -
-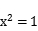 的焦距为( )
的焦距为( )
A.1 B.4 C.2 D.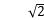
15.已知三角形的两个顶点是椭圆C: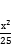 +
+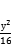 =1的两个焦点,第三个顶点在C上,则该三角形的周长为( )
=1的两个焦点,第三个顶点在C上,则该三角形的周长为( )
A.10 B.20 C.16 D.26
16.在等比数列{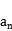 }中,若
}中,若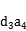 =10,则
=10,则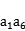 ,+
,+ =( )
=( )
A.100 B.40 C.10 D.20
17.若1名女生和3名男生随机地站成一列,则从前面数第2名是女生的概率为( )
A.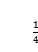 B.
B.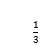 C.
C.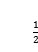 D.
D.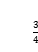
第Ⅱ卷(非选择题,共65分)
二、填空题(本大题共4小题,每小题4分,共16分)
18.已知平面向量a=(1,2),b=(-2,3),2a+3b= .
19.已知直线1和x-y+1=0关于直线x=-2对称,则1的斜率为= .
20.若5条鱼的平均质量为0.8kg,其中3条的质量分别为0.75kg,0.83kg和0.78kg,则其余2条的平均质量为 kg.
21.若不等式|ax+1|<2的解集为{x|- <x<
<x< },则a= .
},则a= .
三.解答题(本大题共4小题,共49分.解答应写出推理、演算步骤)
22. (本小题满分12分)
设{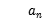 }为等差数列,且
}为等差数列,且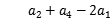 =8.
=8.
(1)求{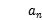 }的公差d;
}的公差d;
(2)若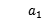 =2,求{
=2,求{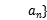 前8项的和
前8项的和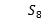 .
.
23.(本小题满分12分)
设直线y=x+1是曲线y=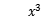 +3
+3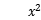 +4x+a的切线,求切点坐标和a的值。
+4x+a的切线,求切点坐标和a的值。
24.(本小题满分12分)
如图,AB与半径为1的圆0相切于A点,AB=3,AB与圆0的弦AC的夹角为50°.求
(1)AC:
 (2)△ABC的面积.(精确到0.01) C
(2)△ABC的面积.(精确到0.01) C
A B
25. (本小题满分13分)
已知关于x,y的方程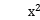 +
+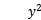 4xsin
4xsin -4ycos
-4ycos =0.
=0.
(1)证明:无论 为何值,方程均表示半径为定长的圆;
为何值,方程均表示半径为定长的圆;
(2)当 =
=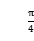 时,判断该圆与直线y=x的位置关系.
时,判断该圆与直线y=x的位置关系.
2017年成人高等学校高起点招生全国统一考试
数学(理工农医类)答案及评分参考
一、选择题
1.A 2.A 3.D 4.A 5.B 6.D 7.A 8.C 9.C 10.D 11.B 12.C 13.B 14.B 15.C 16.D 17.A
二、填空题
18. (-4,13) 19.-1 20.0.82 21.2
三、解答题
22.因为{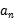 }为等差数列,所以
}为等差数列,所以
(1)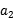 +
+ -2
-2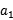 =
=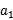 +d+
+d+ +3d-2
+3d-2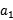
=4d=8,
d=2.
(2)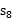 =
=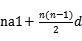
=2 8+
8+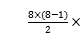 2
2
=72.
23.因为直线y=x+1是曲线的切线,所以y'=3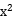 +6x+4=1.解得x=-1.
+6x+4=1.解得x=-1.
当x=-1时,y=0,
即切点坐标为(-1,0).
故0=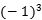 +3
+3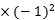 +4
+4 (-1)+a=0
(-1)+a=0
解得a=2.
24.(1)连结OA,作OD⊥AC于D.
 因为AB与圆相切于A点,所以∠OAB=90°. C
因为AB与圆相切于A点,所以∠OAB=90°. C
则∠0AC=90°=50°-40°.

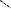 AC=2AD
AC=2AD
=2OA·cos∠OAC D
=2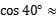 1.54. A B
1.54. A B
(2)S△ABC= AB·ACsin∠BAC
AB·ACsin∠BAC
=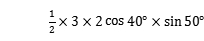
=3os240°
=l.78.
25. (1)证明:
化简原方程得
X2+4xsin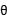 +4sin2
+4sin2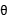 +y2-4y
+y2-4y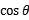 +4
+4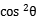 -4sin2
-4sin2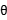 -4
-4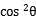 =0,
=0,
(36+2sin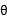 )2+(y-2cos
)2+(y-2cos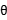 )2=4,
)2=4,
所以,无论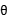 为何值,方程均表示半径为2的圆。
为何值,方程均表示半径为2的圆。
(2)当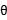 =
= 时,该圆的圆心坐标为O(-
时,该圆的圆心坐标为O(- ,
,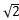 ).
).
圆心O到直线y=x的距离
d=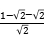 =2=r.
=2=r.
即当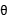 =
= 时,圆与直线y=x相切.
时,圆与直线y=x相切.
以上就是关于“2017年湖南成人高考高起点文史财经类数学考试真”的全部内容,想要了解更多关于学历提升、报考费用、加分政策、志愿填报、录取分数线等的相关问题, 可以随时联系湖南成考网的《专业老师》进行沟通了解。
本文标签:湖南成考文数2017年湖南成人高考高起点文史财经类数学考试真
转载请注明:文章转载自(http://www.acc.gd.cn)
本网所提供的信息仅供学习交流使用
官方信息以《湖南省教育考试院》发布为准